问题 D：车站分级

一条单向的铁路线上，依次有编号为 $1, 2,..., n$ 的 $n$ 个火车站。每个火车站都有一个级别，最低为 $1$ 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 $x$，则始发站、终点站之间所有级别大于等于火车站x的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

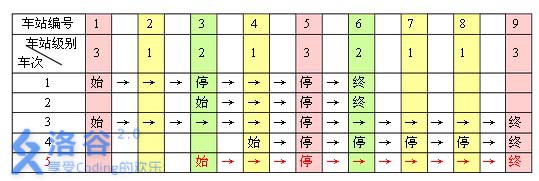
例如，下表是 $5$ 趟车次的运行情况。其中，前 $4$ 趟车次均满足要求，而第 $5$ 趟车次由于停靠了 $3$ 号火车站（ $2$ 级）却未停靠途经的6号火车站（亦为 $2$ 级）而不满足要求。

现有 $m$ 趟车次的运行情况（全部满足要求），试推算这 $n$ 个火车站至少分为几个不同的级别。

每组输入数据的第一行包含 $2$ 个正整数 $n, m$，用一个空格隔开。

第 $i+1$ 行（ $1\le i\le m$）中，首先是一个正整数 $s_i(2\le s_i\le n)$，表示第i趟车次有 $s_i$ 个停靠站；接下来有 $s_i$ 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

数据规模：

对于 $20\%$ 的数据，$1\le n, m\le 10$；

对于 $50\%$ 的数据，$1\le n, m\le 100$；

对于 $100\%$ 的数据，$1\le n, m\le 1000$。

每组输出只有一行，包含一个正整数，即 $n$ 个火车站最少划分的级别数。

9 2
4 1 3 5 6
3 3 5 6

2

9 3
4 1 3 5 6
3 3 5 6
3 1 5 9

3