1733:传送门
文件提交:无需freopen
内存限制:128 MB
时间限制:1.000 S
评测方式:普通裁判
命题人:
提交:5
解决:3
题目描述
在一个神奇空间里有 $N$ 个房间,房间从 $1$ 到 $N$ 编号,每个房间可能有一个或多个传送门,每个传送门都有一个编号,如果相同编号的传送门同时出现在多个房间中,表示这些房间可以互通。
给定两个房间的编号 $A$ 和 $B$,请找出从房间 $A$ 到达房间 $B$ 最少需要经过几个传送门。
例如:$N=3$,$3$ 个房间中传送门的编号分别为:
房间 $1$:$1、4、6$;
房间 $2$:$2、3、4,8$;
房间 $3$:$3、6、9$。
给定两个房间的编号 $A$ 和 $B$,请找出从房间 $A$ 到达房间 $B$ 最少需要经过几个传送门。
例如:$N=3$,$3$ 个房间中传送门的编号分别为:
房间 $1$:$1、4、6$;
房间 $2$:$2、3、4,8$;
房间 $3$:$3、6、9$。
其中房间 $1$ 和房间 $2$ 互通,共用 $4$ 号传送门;房间 $1$ 和房间 $3$互通,共用 $6$ 号传送门;房间 $2$ 和房间 $3$ 互通,共用 $3$ 号传送门;
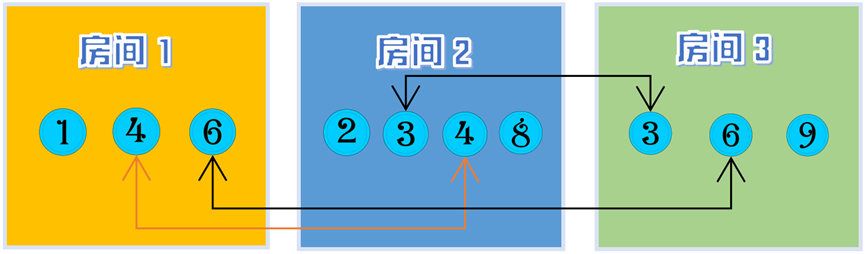
当 $A=1,B=2$,从房间 $1$ 到达房间 $2$,共有两种路线:
路线 $1$:从房间 $1$ 通过 $4$ 号传送门进入房间 $2$,共经过 $1$个传送门;
路线 $2$:从房间 $1$ 通过 $6$ 号传送门进入房间 $3$,再从房间 $3$ 通过 $3$ 号传送门进入房间 $2$,共经过 $2$ 个传送门;
故从房间 $1$ 到达房间 $2$ 最少需要经过 $1$ 个传送门。
输入
第一行输入一个正整数 $N(2\le N\le 20)$,表示房间数量
接下来输入 $N$ 行,每行包含多个正整数( $1\le $正整数 $\le 100$),第 $2$ 行到第 $N+1$ 行依次表示 $1$ 到 $N$ 号房间内所有传送门的编号,正整数之间以一个英文逗号隔开
最后一行输入两个正整数 $A$ 和 $B(1\le A\le N,1\le B\le N$,且 $A$ 不等于 $B$),表示两个房间的编号,正整数之间以一个英文逗号隔开
接下来输入 $N$ 行,每行包含多个正整数( $1\le $正整数 $\le 100$),第 $2$ 行到第 $N+1$ 行依次表示 $1$ 到 $N$ 号房间内所有传送门的编号,正整数之间以一个英文逗号隔开
最后一行输入两个正整数 $A$ 和 $B(1\le A\le N,1\le B\le N$,且 $A$ 不等于 $B$),表示两个房间的编号,正整数之间以一个英文逗号隔开
输出
输出一个整数,表示从房间 $A$ 到达房间 $B$ 最少需要经过几个传送门,如果房间 $A$ 不能到达房间 $B$,则输出 $-1$
样例输入-1 复制
3
1,4,6
2,3,4,8
3,6,9
1,2
样例输出-1 复制
1