1938:蜜蜂与幼虫
文件提交:无需freopen
内存限制:128 MB
时间限制:1.000 S
评测方式:普通裁判
命题人:
提交:2
解决:2
题目描述
蜂巢由一些正六边形的格子组成,这些格子分上下两排,一共有 $n$ 个格子。如果 $n$ 是偶数,则每一排分别有 $\frac{n}{2}$ 个格子,若 $n$ 是奇数,则下排比上排多一个。
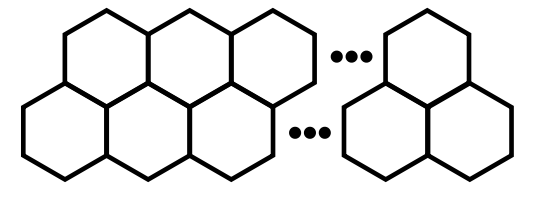
一只成年的蜜蜂,会占据两个相邻的格子,而一只蜜蜂的幼虫只能占据一个格子。
若蜂巢所有的格子都被蜜蜂或幼虫占据了,那么会有多少种不同的方案呢?两个方案若在任何一个格子上的布置有区别,就被看作是不同的方案。
答案可能很大,输出模 $10^9 + 7$的余数。
输入
单个整数:表示 $n$
$1\le n\le 10^6$
输出
单个整数:表示答案。
样例输入-1 复制
4样例输出-1 复制
8