1993:求和问题
文件提交:无需freopen
内存限制:128 MB
时间限制:1.000 S
评测方式:普通裁判
命题人:
提交:10
解决:2
题目描述
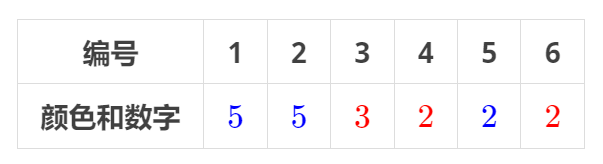
一条狭长的纸带被均匀划分出了 $n$ 个格子,格子编号从 $1$ 到 $n$。每个格子上都染了一种颜色 $color_i$ 用 $[1,m]$ 当中的一个整数表示),并且写了一个数字 $number_i$。
定义一种特殊的三元组:$(x,y,z)$,其中 $x,y,z$ 都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:
1. $x,y,z$ 都是整数,$x<y<z,y-x=z-y$。
2. $color_x=color_z$。
满足上述条件的三元组的分数规定为 $(x+z) \times (number_x+number_z)$。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大,你只要输出整个纸带的分数除以 $10007$ 所得的余数即可。

定义一种特殊的三元组:$(x,y,z)$,其中 $x,y,z$ 都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:
1. $x,y,z$ 都是整数,$x<y<z,y-x=z-y$。
2. $color_x=color_z$。
满足上述条件的三元组的分数规定为 $(x+z) \times (number_x+number_z)$。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大,你只要输出整个纸带的分数除以 $10007$ 所得的余数即可。
输入
第一行是用一个空格隔开的两个正整数 $n$ 和 $m,n$ 表纸带上格子的个数,$m$ 表纸带上颜色的种类数。
第二行有 $n$ 用空格隔开的正整数,第 $i$ 个数字表示纸带上编号为 $i$ 格子上面写的数字 $number_i$。
第二行有 $n$ 用空格隔开的正整数,第 $i$ 个数字表示纸带上编号为 $i$ 格子上面写的数字 $number_i$。
第三行有 $n$ 用空格隔开的正整数,第 $i$ 数字表示纸带上编号为 $i$ 格子染的颜色 $color_i$。
对于第 $1$ 组至第 $2$ 组数据, $1 ≤ n ≤ 100, 1 ≤ m ≤ 5$;
对于第 $3$ 组至第 $4$ 组数据,$1 ≤ n ≤ 3000, 1 ≤ m ≤ 100$;
对于第 $5$ 组至第 $ 6 $ 组数据,$1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000$,且不存在出现次数超过 $ 20 $ 的颜色;
对于全部 $10$ 组数据,$1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000, 1 ≤ color_i ≤ m,1≤number_i≤100000$。
输出
一个整数,表示所求的纸带分数除以 $10007$ 所得的余数。
样例输入-1 复制
6 2
5 5 3 2 2 2
2 2 1 1 2 1样例输出-1 复制
82样例输入-2 复制
15 4
5 10 8 2 2 2 9 9 7 7 5 6 4 2 4
2 2 3 3 4 3 3 2 4 4 4 4 1 1 1样例输出-2 复制
1388提示
NOIP2015 普及组 T3
样例 1 解释
纸带如题目描述中的图所示。
所有满足条件的三元组为:$(1, 3, 5), (4, 5, 6)$。
所以纸带的分数为 $(1 + 5) \times (5 + 2) + (4 + 6) \times (2 + 2) = 42 + 40 = 82$。
