2018:一元二次方程
文件提交:无需freopen
内存限制:128 MB
时间限制:1.000 S
评测方式:普通裁判
命题人:
提交:2
解决:1
题目描述
众所周知,对一元二次方程 $ax ^ 2 + bx + c = 0, (a \neq 0)$,可以用以下方式求实数解:
- 计算 $\Delta = b ^ 2 - 4ac$,则:
1. 若 $\Delta < 0$,则该一元二次方程无实数解。
2. 否则 $\Delta \geq 0$,此时该一元二次方程有两个实数解 $x _ {1, 2} = \frac{-b \pm \sqrt \Delta}{2a}$。
例如:
- $x ^ 2 + x + 1 = 0$ 无实数解,因为 $\Delta = 1 ^ 2 - 4 \times 1 \times 1 = -3 < 0$。
- $x ^ 2 - 2x + 1 = 0$ 有两相等实数解 $x _ {1, 2} = 1$。
- $x ^ 2 - 3x + 2 = 0$ 有两互异实数解 $x _ 1 = 1, x _ 2 = 2$。
在题面描述中 $a$ 和 $b$ 的最大公因数使用 $\gcd(a, b)$ 表示。例如 $12$ 和 $18$ 的最大公因数是 $6$,即 $\gcd(12, 18) = 6$。
## 题目描述
现在给定一个一元二次方程的系数 $a, b, c$,其中 $a, b, c$ **均为整数且 $a \neq 0$**。你需要判断一元二次方程 $a x ^ 2 + bx + c = 0$ 是否有实数解,并按要求的格式输出。
**在本题中输出有理数 $v$ 时须遵循以下规则:**
- 由有理数的定义,存在唯一的两个整数 $p$ 和 $q$,满足 $q > 0$,$\gcd(p, q) = 1$ 且 $v = \frac pq$。
- 若 $q = 1$,则输出 {p},否则输出 {p}/{q},其中 {n} 代表整数 $n$ 的值;
- 例如:
- 当 $v = -0.5$ 时,$p$ 和 $q$ 的值分别为 $-1$ 和 $2$,则应输出 -1/2;
- 当 $v = 0$ 时,$p$ 和 $q$ 的值分别为 $0$ 和 $1$,则应输出 0。
**对于方程的求解,分两种情况讨论:**
1. 若 $\Delta = b ^ 2 - 4ac < 0$,则表明方程无实数解,此时你应当输出 NO;
2. 否则 $\Delta \geq 0$,此时方程有两解(可能相等),记其中较大者为 $x$,则:
1. 若 $x$ 为有理数,则按有理数的格式输出 $x$。
2. 否则根据上文公式,$x$ 可以被**唯一**表示为 $x = q _ 1 + q _ 2 \sqrt r$ 的形式,其中:
- $q _ 1, q _ 2$ 为有理数,且 $q _ 2 > 0$;
- $r$ 为正整数且 $r > 1$,且不存在正整数 $d > 1$ 使 $d ^ 2 \mid r$(即 $r$ 不应是 $d ^ 2$ 的倍数);
此时:
1. 若 $q _ 1 \neq 0$,则按有理数的格式输出 $q _ 1$,并再输出一个加号 `+`;
2. 否则跳过这一步输出;
随后:
1. 若 $q _ 2 = 1$,则输出 sqrt({r});
2. 否则若 $q _ 2$ 为整数,则输出 {q2}*sqrt({r});
3. 否则若 $q _ 3 = \frac 1{q _ 2}$ 为整数,则输出 sqrt({r})/{q3};
4. 否则可以证明存在唯一整数 $c, d$ 满足 $c, d > 1, \gcd(c, d) = 1$ 且 $q _ 2 = \frac cd$,此时输出 {c}*sqrt({r})/{d};
上述表示中 {n} 代表整数 {n} 的值,详见样例。
如果方程有实数解,则按要求的格式输出两个实数解中的较大者。否则若方程没有实数解,则输出 NO。
- 计算 $\Delta = b ^ 2 - 4ac$,则:
1. 若 $\Delta < 0$,则该一元二次方程无实数解。
2. 否则 $\Delta \geq 0$,此时该一元二次方程有两个实数解 $x _ {1, 2} = \frac{-b \pm \sqrt \Delta}{2a}$。
例如:
- $x ^ 2 + x + 1 = 0$ 无实数解,因为 $\Delta = 1 ^ 2 - 4 \times 1 \times 1 = -3 < 0$。
- $x ^ 2 - 2x + 1 = 0$ 有两相等实数解 $x _ {1, 2} = 1$。
- $x ^ 2 - 3x + 2 = 0$ 有两互异实数解 $x _ 1 = 1, x _ 2 = 2$。
在题面描述中 $a$ 和 $b$ 的最大公因数使用 $\gcd(a, b)$ 表示。例如 $12$ 和 $18$ 的最大公因数是 $6$,即 $\gcd(12, 18) = 6$。
## 题目描述
现在给定一个一元二次方程的系数 $a, b, c$,其中 $a, b, c$ **均为整数且 $a \neq 0$**。你需要判断一元二次方程 $a x ^ 2 + bx + c = 0$ 是否有实数解,并按要求的格式输出。
**在本题中输出有理数 $v$ 时须遵循以下规则:**
- 由有理数的定义,存在唯一的两个整数 $p$ 和 $q$,满足 $q > 0$,$\gcd(p, q) = 1$ 且 $v = \frac pq$。
- 若 $q = 1$,则输出 {p},否则输出 {p}/{q},其中 {n} 代表整数 $n$ 的值;
- 例如:
- 当 $v = -0.5$ 时,$p$ 和 $q$ 的值分别为 $-1$ 和 $2$,则应输出 -1/2;
- 当 $v = 0$ 时,$p$ 和 $q$ 的值分别为 $0$ 和 $1$,则应输出 0。
**对于方程的求解,分两种情况讨论:**
1. 若 $\Delta = b ^ 2 - 4ac < 0$,则表明方程无实数解,此时你应当输出 NO;
2. 否则 $\Delta \geq 0$,此时方程有两解(可能相等),记其中较大者为 $x$,则:
1. 若 $x$ 为有理数,则按有理数的格式输出 $x$。
2. 否则根据上文公式,$x$ 可以被**唯一**表示为 $x = q _ 1 + q _ 2 \sqrt r$ 的形式,其中:
- $q _ 1, q _ 2$ 为有理数,且 $q _ 2 > 0$;
- $r$ 为正整数且 $r > 1$,且不存在正整数 $d > 1$ 使 $d ^ 2 \mid r$(即 $r$ 不应是 $d ^ 2$ 的倍数);
此时:
1. 若 $q _ 1 \neq 0$,则按有理数的格式输出 $q _ 1$,并再输出一个加号 `+`;
2. 否则跳过这一步输出;
随后:
1. 若 $q _ 2 = 1$,则输出 sqrt({r});
2. 否则若 $q _ 2$ 为整数,则输出 {q2}*sqrt({r});
3. 否则若 $q _ 3 = \frac 1{q _ 2}$ 为整数,则输出 sqrt({r})/{q3};
4. 否则可以证明存在唯一整数 $c, d$ 满足 $c, d > 1, \gcd(c, d) = 1$ 且 $q _ 2 = \frac cd$,此时输出 {c}*sqrt({r})/{d};
上述表示中 {n} 代表整数 {n} 的值,详见样例。
如果方程有实数解,则按要求的格式输出两个实数解中的较大者。否则若方程没有实数解,则输出 NO。
输入
输入的第一行包含两个正整数 $T, M$,分别表示方程数和系数的绝对值上限。
接下来 $T$ 行,每行包含三个整数 $a, b, c$。
**【数据范围】**
对于所有数据有:$1 \leq T \leq 5000$,$1 \leq M \leq 10 ^ 3$,$|a|,|b|,|c| \leq M$,$a \neq 0$。
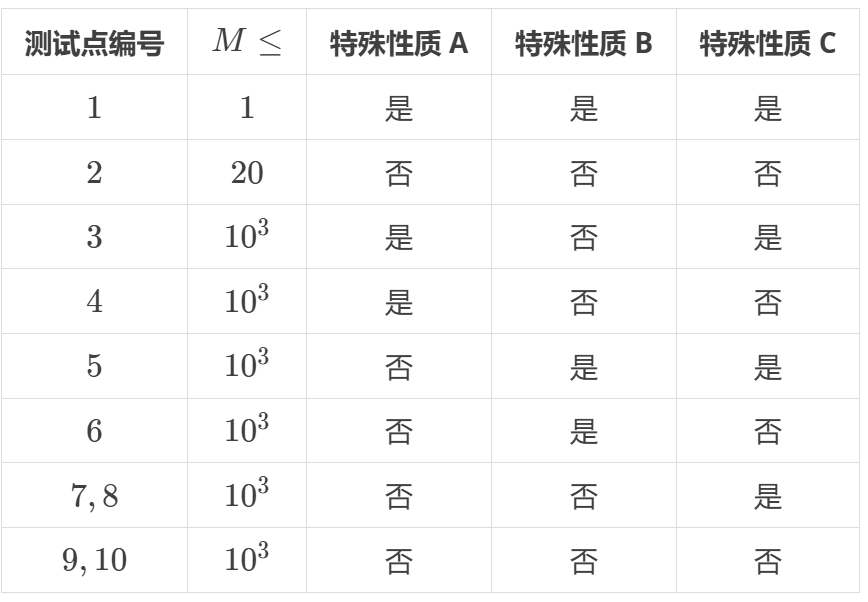
其中:
- 特殊性质 A:保证 $b = 0$;
- 特殊性质 B:保证 $c = 0$;
- 特殊性质 C:如果方程有解,那么方程的两个解都是整数。
输出
输出 $T$ 行,每行包含一个字符串,表示对应询问的答案,格式如题面所述。
**每行输出的字符串中间不应包含任何空格**。
**每行输出的字符串中间不应包含任何空格**。
样例输入-1 复制
9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1样例输出-1 复制
1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2提示
CSP-J 2023 T3
