2043：蒜头君的要塞

在浩瀚的银河系中，蒜头君统治着无数星系，但他不满足于现状，计划进一步扩展他的星际帝国。他决定在宇宙中的关键位置建立战略基地，从而增强对不同星系的控制。

在广阔的星系版图上，存在 $n$ 个星际要塞，每个要塞的位置由其坐标 $(x,y)$ 确定。为了最大化控制范围，蒜头君需要选择从 $1$ 到 $n$ 中选出 $k$ 个要塞，并在这些要塞之间建立一个新的指挥中心 $P(x,y)$，以确保从指挥中心到这些要塞的曼哈顿距离之和最小。

两个点 $(a,b),(c,d)$ 的曼哈顿距离为 $|a-c|+|b-d|$

你需要帮助蒜头君计算在不同选择方案下的最优指挥中心位置，使得他能够最有效地统治整个星域。

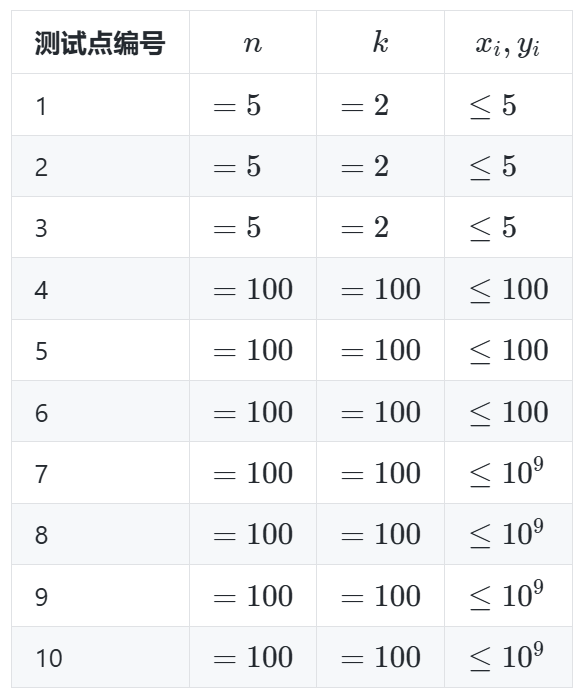
第一行包含两个整数 $n，k$，分别表示星际要塞的数量和最大选择的要塞数量

接下来的 $n$ 行，每行包含两个整数，表示每个要塞的坐标 $(x,y)$

4 3 
1 3
2 4
3 5
4 2

0
2
4